算数 組み合わせ 174990-算数 組み合わせ

小6算数 場合の数 2 指導アイデア みんなの教育技術
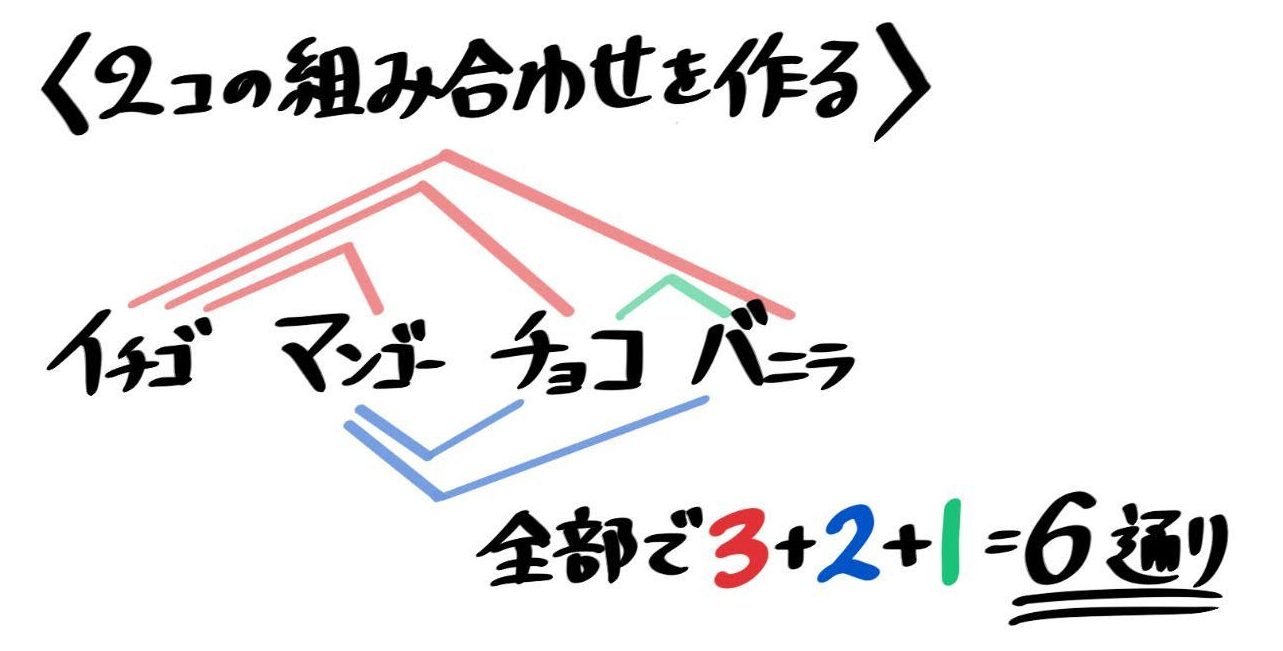
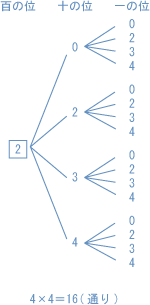
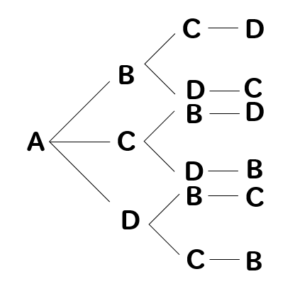
組分け(グループ分け)問題の解法 そして、その各々の組み分け先に 空きがあっても良いか否かで更に種類が2倍に増える ので、計8種類にもなります。 1:区別がつくもの→区別がつくもの 2:区別がつくもの→区別がつかないもの 3:区別がつかない組み合わせとは 「並べない順列」というのも少し日本語がおかしいですが、つまり組み合わせとは 「選ぶだけ」の場合の数 の事を言うんです。 たとえば順列が「7個のボール中から→3個選んで→1列に並べる」という場合の数を数えたのに対し、組み合わせは「7個のボールの中から→3個を選ぶ」という場合の数だけを数えるんです。 これが順列と組み合わせの違い
算数 組み合わせ
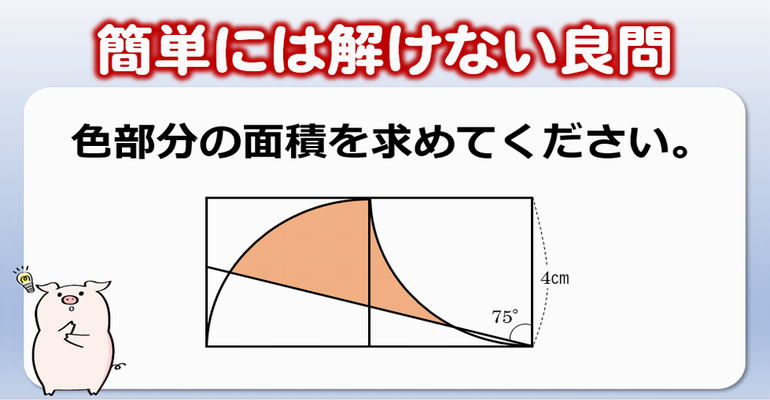
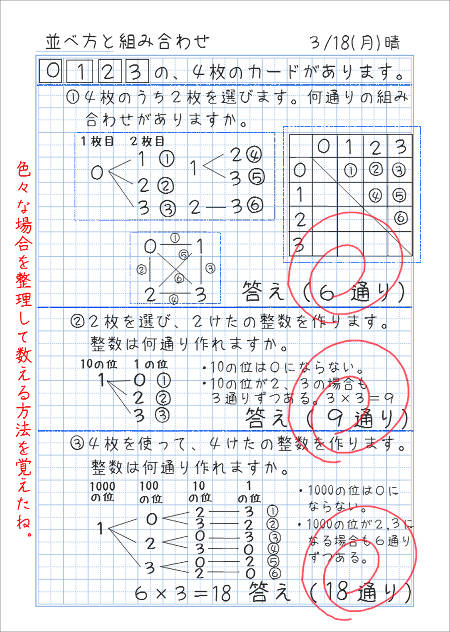
算数 組み合わせ- 組み合わせた図形の面積 15年8月14日 / Last updated 19年7月18日 doramaru 算数・計算 面積 4年生の算数 複雑な長方形を組み合わせた図形の面積を求めます。 組み合わせとは? 組み合わせ 異なる \( n \) 個のものの中から \( r \) 個取り出したときの、組み合わせの数のこと(順序は考慮しない)。 \( n \) 個のものの中から \( r \) 個取り出すときの組み合わせの総数を \( \displaystyle \large{ \color{red} {_n \mathrm{C}_r} } \) と表す。

小6算数 ならべ方と組み合わせ方 学習プリント 練習問題 無料ダウンロード印刷
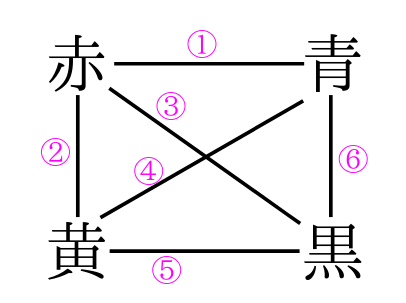
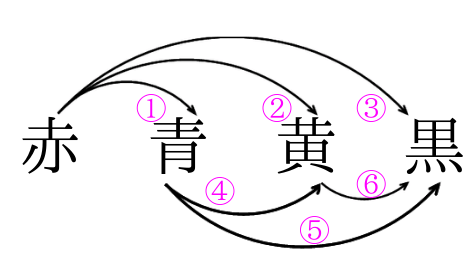
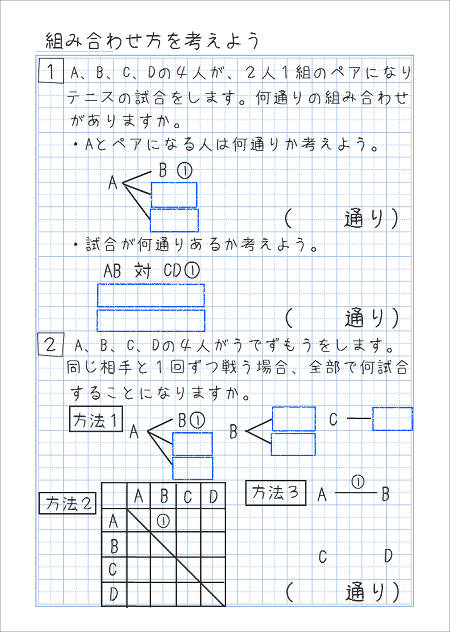
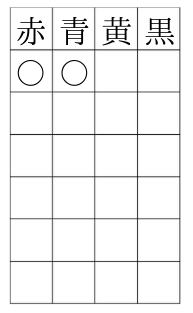
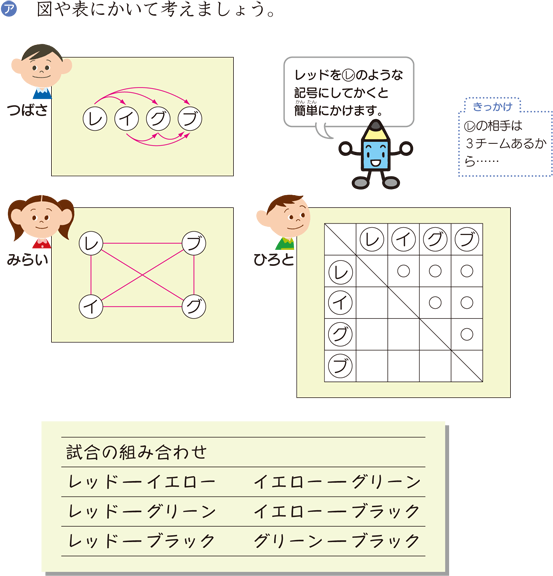
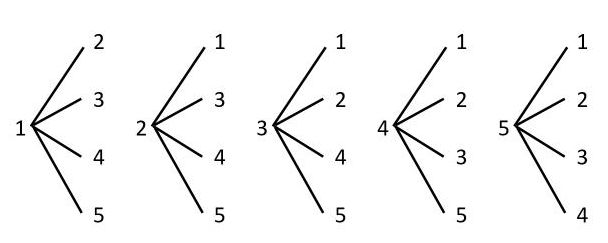
組み合わせの数え方① 横に赤、青、黄、黒の文字を書きます。 次に左から順番に下の図のように線で結びます。 後はその線の数を数えます。 線の数は6本なので、6通りという事が分かります。 コツは番号を振っている順に数えることです。 適当に数えていくと、どこまで数えたのか分からなくなってしまいます。 この数え方は、いくつかのモノから2つ順番を考えるときには樹形図を使って考えていきましょう! まず、Aが先頭になる並び方から考えてみましょう。 すると、このように ABC、ACBと2通りの並べ方があることがわかりますね。 よって、(1)の答えは2通りとなります。 次に、全体を考えていきます。 Aを先頭にして並べる方法が2通りでした。 ということは同じように考えて Bを先頭にした場合も2通り 小6算数 小6算数「並べ方と組合せ方」の問題 どこよりも簡単な解き方・求め方 kazunokazu 21年7月5日 / 22年2月3日
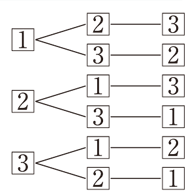
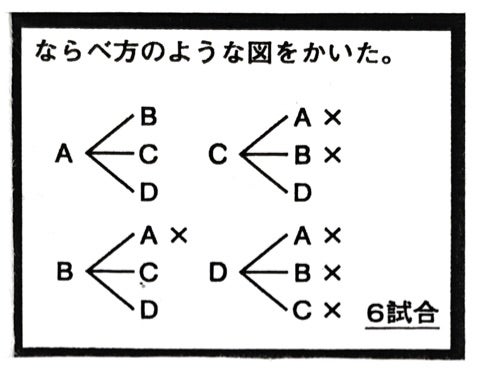
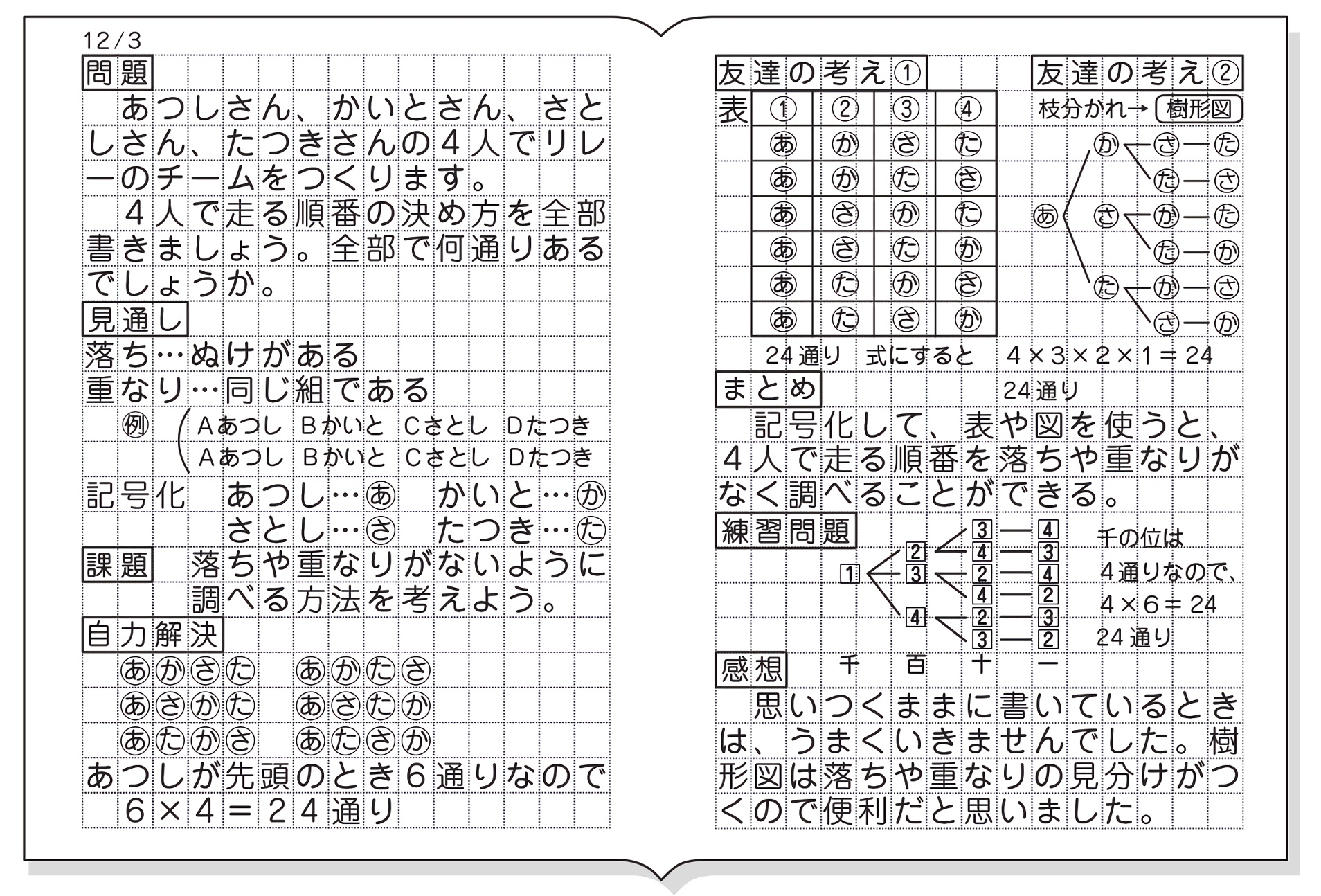
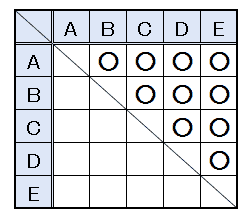
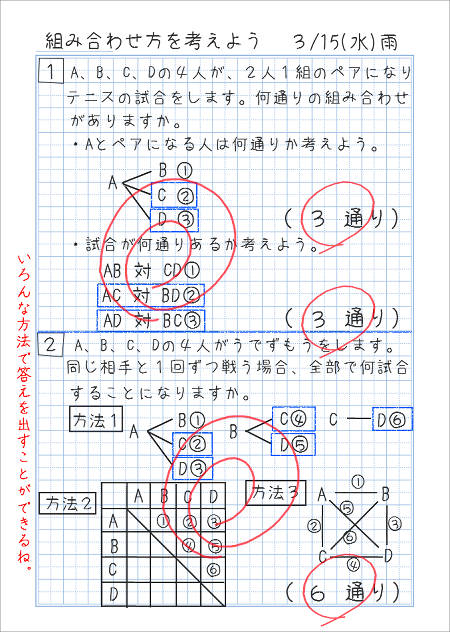
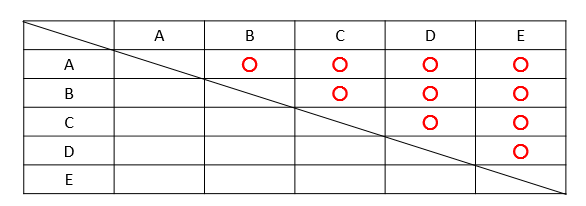
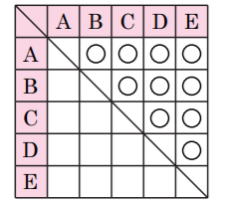
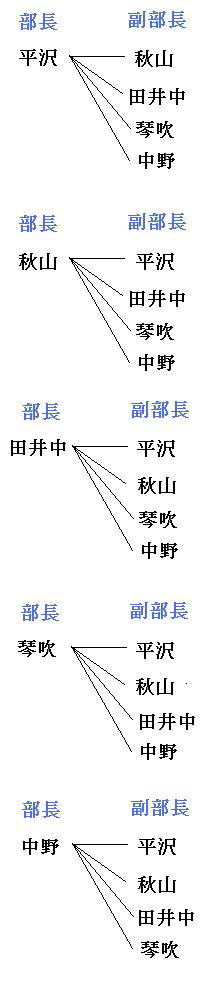
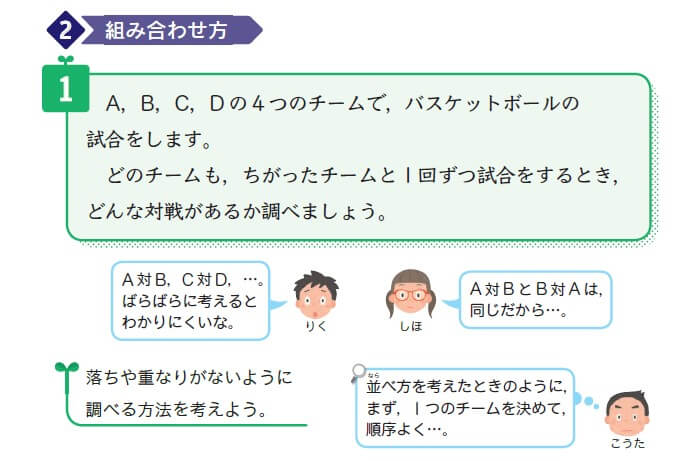
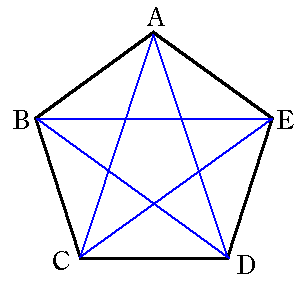
並べ方と組み合わせ方 小学校6年 算数 順列について、落ちや重なりのないように調べる方法を考え、その方法を理解する。 (1) 並べ方 (2組み合わせの問題|考え方と解き方 <下記問題の解説ファイル> ※6年上第4回ステップアップ例題は最下段にあります。 (例題1)箱の中に。 赤玉が2個,白玉が2個,青玉が1個入っています。 この中から3個の玉を選ぶとき,玉の選び方は。 全部で何通り組み合わせの問題一覧(場合の数) ★学習内容:中学受験の「場合の数に関する問題」の主なるパターン,和の法則,積の法則,ならべ方(順列),組み合わせ,試合の方法と試合数など ・箱の中に赤玉が2個,白玉が2個,青玉が1固入っています。 この中から3個の玉を選ぶとき,玉の選び方は,全部で何通りありますか。 ・A, B, C, D, Eの5人がいます。 この5人の中から
算数 組み合わせのギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  |  |
 |  | |
 |  | |
「算数 組み合わせ」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 | ||
「算数 組み合わせ」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 | ||
 |  |  |
「算数 組み合わせ」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 | ||
「算数 組み合わせ」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  |  |
「算数 組み合わせ」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「算数 組み合わせ」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  | |
「算数 組み合わせ」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | |
「算数 組み合わせ」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  | |
「算数 組み合わせ」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  |  |
「算数 組み合わせ」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  |  |
「算数 組み合わせ」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |
①:「この中から2枚を使って 2ケタの数字を作る 場合、作れる数字は何通りあるか? 」 ②:「この中から 2枚のカードを選ぶ 場合、選び方は何通りあるか? 」 この2種類の問題では、それぞれ答えが変わってきます。 ①は 順列 で、答えは 5 P 2 =5×4=通り ②は 組み合わせ で、答えは 5 C 2 =5×4÷2=10通りになります。 今回は、そんな順列と組み合わせの数の考え方についてです このページは、このような人へ向けた内容となっています 組み合わせの計算(\\({}_nC_r\\))が苦手 組み合わせの計算(\\({}_nC_r\\))をよく間違えてしまう 計算量が多くて嫌いなので、もっと簡単に計算できる方法を知りたい 高校数学の組み合わせの単元で登場するコンビネーション(\\({}_nC_r
Incoming Term: 算数 組み合わせ, 算数 組み合わせ 公式, 算数 組み合わせ 問題, 算数 組み合わせ 何通り, 算数 組み合わせ 考え方, 算数 組み合わせ 計算,




コメント
コメントを投稿